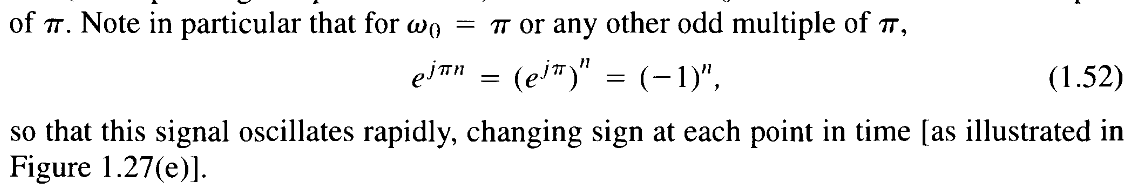aliasing in discrete time

rwsignal8nisan The exponential with frequency ω₀ is identical to the exponentials with frequencies ω₀ ± 2π, ω₀ ± 4π, ω₀ ± 6π, and so on. This is the key concept of aliasing in discrete-time. Because the signal is only sampled at discrete points in time, you can’t distinguish between a signal with frequency ω₀ and signals whose frequencies differ by integer multiples of 2π.

• This holds true because n is always and integer in DT. Yet for CT, this wouldnt hold true almost for all t. Therefore, in continuous time: e^(j(ω₀ + 2π)t) ≠ e^(jω₀t) (in general)

Why aliasing exist?

Reason for aliasing in discrete-time is that sampling loses information

How DT sequence reacts to increase in w?

1. As we increase ω₀ from 0, we obtain signals that oscillate more and more rapidly until we reach ω₀ = π. This describes the behavior in the first half of the fundamental frequency range. From ω₀ = 0 (a constant signal) to ω₀ = π, increasing the frequency does increase the oscillation rate, as you’d expect.
2. If we continue to increase ω₀, we decrease the rate of oscillation until we reach ω₀ = 2π, which produces the same constant sequence as ω₀ = 0. This is where aliasing manifests. Beyond ω₀ = π, increasing the frequency actually decreases the oscillation rate. The frequencies are “folding back” due to aliasing. ω₀ = 2π is equivalent to ω₀ = 0 (both are constant signals), ω₀ = 2π + Δ is equivalent to ω₀ = Δ, and so on.
3. Frequencies near odd multiples of π represent the fastest possible oscillations in discrete-time. The low frequency (slowly varying) DT exponentials have values of ω₀ near 0, 2π and any other even multiple of π. Because of aliasing, frequencies near even multiples of π are all equivalent to low frequencies (slow oscillations). Why?questionsdead