equations of a system, SISO and MIMO

rw

• ẋ = Ax + Bu: This is the state equation. It describes how the internal state of the system (x) changes over time.

  • x: The state vector. This is a vector of variables that completely describe the system’s internal condition at any given time. Think of it like the system’s memory. The dimension of x defines the order of the system. If x has n elements, it’s an nth-order system.
  • ẋ: The time derivative of the state vector (how the state is changing).
  • A: The state matrix (or system matrix). This is a square matrix (n x n, where n is the order of the system) that determines how the current state influences its own rate of change. It governs the system’s internal dynamics without considering the input.
  • B: The input matrix. This matrix describes how the input (u) affects the rate of change of the state. In the initial description, it’s presented as if it has a single column, which correspond to a Single Input.
  • u: The input (or control) signal. In the single-input case, this is a scalar (a single number).

• y = Cx + Du: This is the output equation. It describes how the output (y) of the system is related to the state (x) and the input (u).

  • y: The output signal. In the single-output case, this is a scalar.
  • C: The output matrix. This matrix determines how the state variables are combined to produce the output.
  • D: The feedforward (or feedthrough) matrix. This matrix represents a direct path from the input to the output, bypassing the state variables. It’s often zero in many systems (meaning the input doesn’t directly affect the output without going through the state).

SISO

The initial description, with u, y ∈ R, explicitly states that the system is single-input, single-output (SISO). This means:

• u is a single scalar value (a single input signal).
• y is a single scalar value (a single output signal).
• Because of this, B is a column vector, and C is a row vector, and D is a scalar.

What if MIMO?

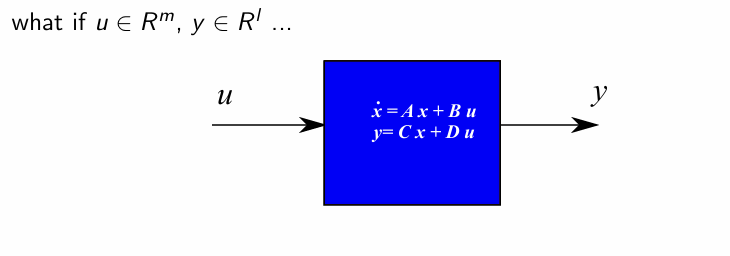
what if u ∈ R^m, y ∈ R^l ...: This is the crucial question. It asks what happens to the state-space representation if we have:

• u ∈ R^m: The input u is now a vector of m different input signals. This means we have multiple inputs.
• y ∈ R^l: The output y is now a vector of l different output signals. This means we have multiple outputs.

how the matrices would change?

A remains and n x n matrix. The internal dynamics of the system, represented by A, don’t fundamentally change just because we have more inputs or outputs. The order of the system is determined by the number of state variables (n), which remains the same.

• B (Input Matrix): Becomes an n x m matrix.
  • n rows (corresponding to the n state variables).
  • m columns (corresponding to the m input signals). Each column of B describes how a particular input affects the rate of change of all the state variables.
• C (Output Matrix): Becomes an l x n matrix.
  • l rows (corresponding to the l output signals).
  • n columns (corresponding to the n state variables). Each row of C describes how all the state variables are combined to produce a particular output.
• D (Feedforward Matrix): Becomes an l x m matrix.
  • l rows (corresponding to the l output signals).
  • m columns (corresponding to the m input signals). Each element D(i, j) represents the direct influence of the j-th input on the i-th output.

transfer function H(jw)