- A system is considered stable if small inputs lead to responses that do not diverge.
- This essentially means that minor perturbations in the input should not cause unbounded growth in the system’s response.
BIBO Stability (Bounded input bounded output)
Every bounded input produces a bounded output. If an input is bounded (i.e., its magnitude does not grow infinitely), then the system’s output must also be bounded and cannot diverge (doesnt go to infinity).
Understanding Bounded Input: An input signal is bounded if you can draw two horizontal lines on its graph, one at +B and one at −B, and the entire signal stays between those lines for all time.
- Bounded examples: A constant value (like x(t)=1 used in Example 13), a sine wave, a decaying exponential.
- Unbounded examples: A signal like x(t)=t (a ramp), x(t)=et (a growing exponential), because these go towards infinity as time goes on. Check the example 2.
example to unstable system
- A bank account balance model demonstrates an unstable system:
- If an initial deposit is made and there are no withdrawals, the deposit grows indefinitely.
- This corresponds to a difference equation:
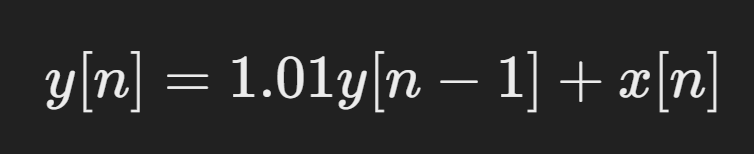
Physical systems often stabilize due to energy dissipation (e.g., friction).
Examples
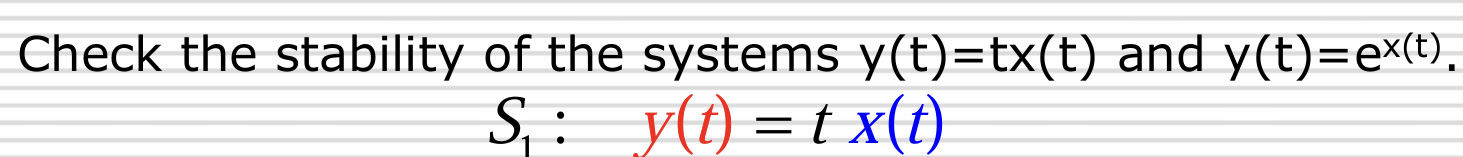Small changes in input makes output diverge?
A bounded input: x(t) = 1. This makes y(t) = t. Wait. y = t is unbounded. Than this system is not bibo stable.
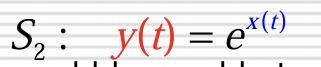You cant find a bounded x(t) such that e^x(t) is unbounded.
