This note summarizes Richard Swinburne’s explanation of Bayes’s Theorem from The Existence of God . The theorem provides a formal framework for understanding how evidence impacts the probability of a hypothesis.
The Theorem and Its Components 🎲
Bayes’s Theorem formalizes the relationship between a hypothesis’s probability and new evidence. The formula is:
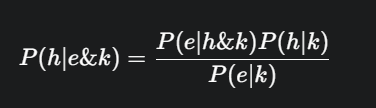
-
P(h∣e&k) (Posterior Probability): This is the final probability of the hypothesis (h) after considering the new evidence (e) and background knowledge (k).
-
P(h∣k) (Prior Probability): This is the initial probability of the hypothesis before considering the evidence. It’s based on factors like simplicity and fit with background knowledge. If there’s no background knowledge, it’s called the intrinsic probability and depends mainly on simplicity.
-
P(e∣h&k) (Predictive Power): This measures how likely the evidence (e) is if the hypothesis (h) is true . A hypothesis is stronger if it makes the evidence more expected.
-
P(e∣k) (Prior Probability of the Evidence): This is the probability of the evidence occurring on its own, regardless of the hypothesis. The more surprising or otherwise inexplicable the evidence is, the lower this value is, and the more the evidence supports the hypothesis.
Swinburne notes that he uses the theorem not for exact numerical calculations, but for making judgments about comparative probability (i.e., whether one hypothesis is more probable than another).
Key Implications of the Theorem
1. The Irrelevance of “Prediction”
A common idea is that a hypothesis must successfully predict a future event to be confirmed. Swinburne argues this is incorrect.
-
According to the theorem, the timing of the evidence’s discovery doesn’t matter. What matters is the logical relationship between the hypothesis and the evidence.
-
A hypothesis can be confirmed by evidence that was already known. For example, Newton’s theory was highly probable because it explained existing laws (like Kepler’s), not because it made new predictions .
2. The “Relevance Criterion”
A crucial principle derived from the theorem is that evidence confirms a hypothesis if and only if that evidence is more likely to occur if the hypothesis is true than if it is false.
-
This means an argument from evidence (e) to a hypothesis (h) is a good C-inductive argument (an argument that increases the probability of its conclusion) only if e is more likely given h is true than given h is false.
-
Example: Fingerprints on a safe are evidence against Jones only if it’s more probable for his prints to be there if he committed the crime than if he didn’t.
Application to Theism ✝️
Swinburne outlines his plan to use this framework to assess the probability of God’s existence .
-
Hypothesis (h): Theism (“God exists”).
-
Evidence (e): The various features of the world that are presented as evidence for or against God’s existence.
-
Prior Probability (P(h∣k)): Since theism is a hypothesis of vast scope, there is no background knowledge to fit with. Therefore, its intrinsic probability depends almost entirely on its simplicity. Swinburne will argue that theism is a very simple hypothesis.
-
Explanatory Power: The core of his argument will be to assess, for each piece of evidence, how probable it is that the evidence would occur if there is a God versus if there is not. This will determine the evidential force of each argument.
Bkz: How can reason lead to god • contingency argument • Matematik