Vector spaces are not only objects but rules

📌 Core Concept: The “Operations” Trap

A common misconception is thinking that a “good” set (like $\mathbb{R}$ or ${\mathbb{R}}^n$) automatically guarantees a Vector Space. It does not.

A Vector Space is a triplet $(V,\oplus ,\odot )$:

1. A Set ($V$)
2. An Addition Operation ($\oplus$)
3. A Scalar Multiplication Operation ($\odot$)

If the operations are redefined non-standardly, the structure often breaks.

⚠️ Counter-Example: “Subtraction” as Addition

Context: Example 5 from lecture slides. 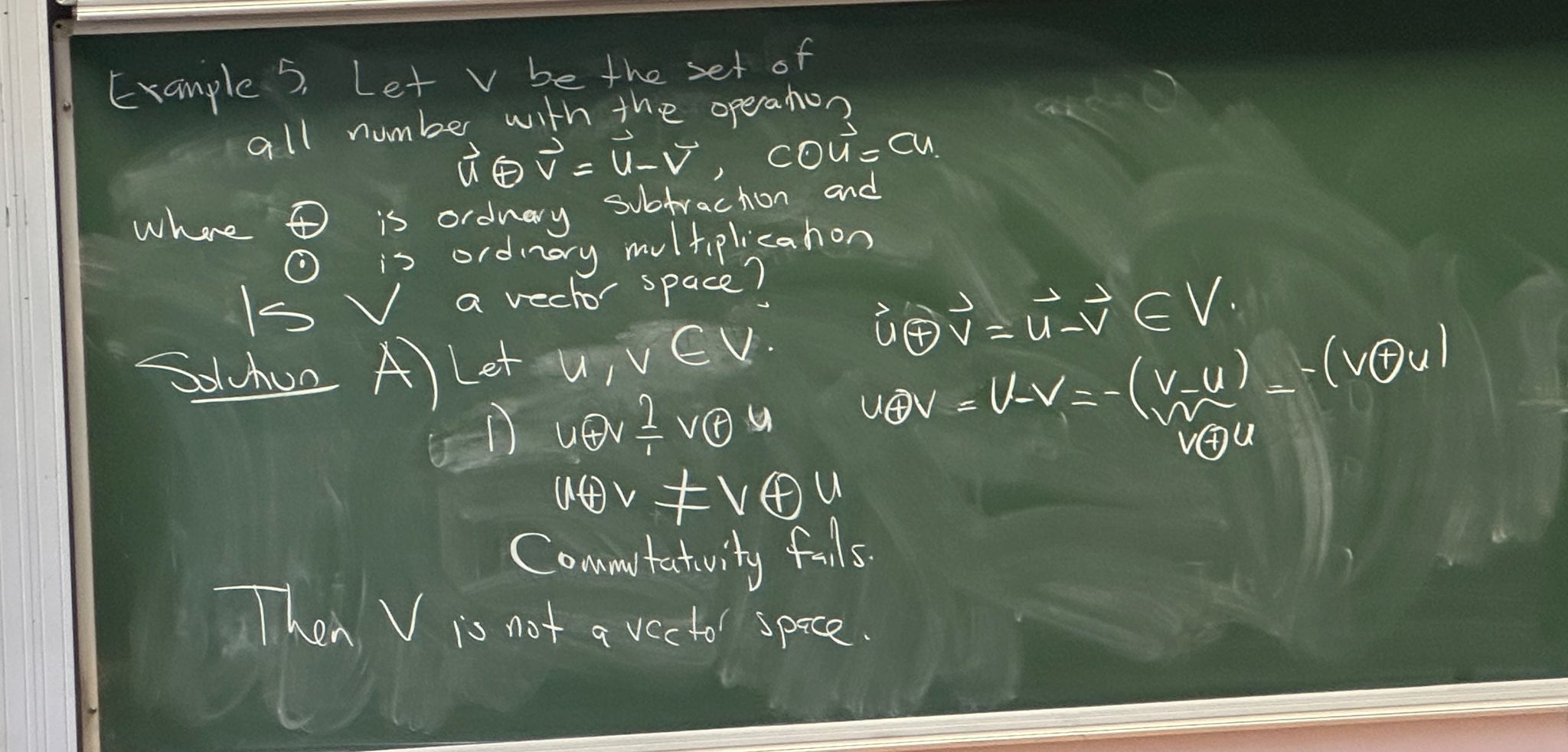Scenario:

• Set ($V$): All real numbers ($\mathbb{R}$).
• Operation ($\oplus$): Defined as ordinary subtraction ($u\oplus v=u-v$).
• Question: Is $V$ a vector space under this operation?

Analysis (The Failure): For $V$ to be a vector space, it must satisfy Commutativity of Addition (Axiom 1): $u\oplus v=v\oplus u$

Let’s test it:

• LHS: $u\oplus v=u-v$
• RHS: $v\oplus u=v-u$

Since $u-v\ne v-u$ (unless $u=v$), Commutativity Fails.

Conclusion: Even though the set contains all real numbers, the operation definition destroys the vector space structure.

Takeaway: Always check the 10 Axioms against the specific operations given. Never assume a set is a vector space just because it looks familiar.

Bkz: Matematik • Matrix Transformations • Lagrange Multipliers